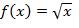Lesson 0: Quick Review of Functions

The domain of a function f(x) is the set of all values of x for which f(x) is defined. Most common functions of real numbers (unless otherwise noted, we shall stick to real numbers for the time being) have a range extending from -∞ to +∞¹. Some functions, however, do not have this full range. For example, the function

Only has a domain of [0, ∞) (also written as 0 ≤ x < ∞).

The range of a function are the value which the function can output. Again, many functions have a range that spans the entire real number line. Some functions, however, only have a limited range. The function f(x) = sin x, for example, only has a range of [-1, 1].

In the equation y = f(x), f(x) is considered a function if and only if for each value of x in its domain, there exists one and only one value for y.

A function can be defined explicitly or implicitly. The equation y = f(x) defines y as a function of x explicitly. However, as an example of a simple implicitly defined function, we can use the equation y + x = 1. This equation implicitly defines y as a function of x (in this particular case, x could also be said to be implicitly defined as a function of y). If we rearrange the equation, we can get y = 1 - x, which is of the form y = f(x) (y here is being defined explicitly as a function of x) where f(x) = 1 - x.

Not all equations, however, define a function. The equation for the unit circle centered on the origin, for example, is

This equation does not define a y as a function of x (and for the same reason, it does not define x as a function of y). To see why, we should rearrange the equation to get y by itself. To do this, we subtract x^2 from both sides and then take plus or minus the square root:

The reason we must take plus or minus the square root is because the result of the original equation remains unchanged if we change the value we have for y to its negative. For example [1/Sqrt(2)]^2 + [1/Sqrt(2)]^2 = [-1/Sqrt(2)]^2 + [1/Sqrt(2)]^2 = 1. The result is the same if we use plus or minus 1/Sqrt(2). Because this equation cannot find a unique value for y for each value of x in the domain, it is not a function. To visually see why this is, consider the graph of the unit circle:

For each value along the x (horizontal) axis, there are two values along the y (vertical) axis. The two exceptions are at the points x = 1 and x = -1. Take for example, x = 0 (the origin). You can choose to go up from the origin, and eventually hit the graph at the y value y = 1, or you can choose to go down from the origin and eventually hit the graph at y = -1. Because there are two value of y corresponding to most values of x, this fails to be a graph of a function (only one value of x corresponding to more than one y is enough for an equation or graph to not define a function).

Now we can choose to only take the positive values of y in the equation, which would correspond only to the top half of the circle, and this would define a function.

A visual test to see if a graph defines a function or not is to take a vertical line and pass it over the entire domain of the graph. If there is any point along the x axis in which the vertical line hits more than one point on the graph, then the graph does not define a function. If no such point exists, then the graph does define a function. This is called the vertical-line test.

I am here of course assuming an understanding of the basics of graphing. If anyone needs help with slopes and intercepts and tests for symmetry etc. let me know and I will try to accommodate. I will help with logarithms and exponentials, when the time comes, but I hate trig. so if anyone needs help with that, if you have a specific question, I could probably answer it, but most likely I will not dedicate a whole blog entry to it.

Most functions have inverses (pretty much an inverse can be defined in some form or another, if not explicitly); however, not all functions have inverse functions. That is to say that just because f(x) is a function does not mean that f ^ -1 (x) is a function. The example of the unit circle above shows, for example, the the inverse of the square (plus or minus the square root) is not a function. In general, is multiple values of x give the same value of y (which is permissible in functions), then its inverse is not a function. To visually see if the inverse of the graph of a function (or equation) is itself a function, one can perform a horizontal-line test (which is the same as the vertical line test, only with a horizontal line running along the entirety of the range of the graph).

My plan is to begin actual calculus on my next post by starting with the basics of limits.

Footnotes

¹ This range is expressed as (-∞, +∞) where the parentheses indicate an open interval (square brackets indicated a closed interval--since infinity is not a number, it is impossible to have the interval closed on a side with either positive or negative infinity). It can also be expressed as -∞ < x < +∞ (closed intervals will use a less than or equal to sign). 

Intro

This will be the first (hopefully) in a series of math and physics blogs that I intend to create as a way to make physics and higher-level math available and accessible to the general public for free. For now, I will assume a working knowledge of algebra, trigonometry, and geometry. If the need arises and time permitting I will create blogs to outline the basics of those areas of mathematics.

While I encourage people to ask questions about things they do not understand in the comments section, please understand that I am doing this for free in my spare time. I will try to answer as many questions as possible as quickly as possible, but I also have a full time job and other things going on in my life. So please respect that if I don't respond to your question right away.

I will try to make sure that all the information I post in this blog is considered common knowledge in math and science related academia. Graphs that I post will be produced with Mathematica (unless otherwise noted) and equations will be rendered using either Mathematica or (usually) Microsoft Word, which has a great process for rendering equations. I'm not sure how exactly integrating equations and graphs into my posts is going to work, so I may need to try a few times before getting my posts to look the way I want them to. If anyone feels I have mis-used copyrighted materials in any way, please inform me and I will take the appropriate actions.