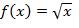Lesson 1.4: Continuity, One-Sided Limits, and the Existence of Limits

Take a look at the function

This function has a discontinuity at the point x = 1 called a jump discontinuity because the graph "jumps" from one value to another (note that the function ƒ(x) = |x|/x that was presented in Lesson 1.3 also displays a jump discontinuity at the point x = 0). You can see this in the plot of the function:

Figure 1.4

In Figure 1.4, the closed circle represents the final point on the line where the function is defined, whereas, the open circle represents the fact that the function is defined on that line only up to that point, but not including it. Because of the jump discontinuity, the limit of the function as x approaches 1 does not exist. However, the function does have two one-sided limits:

The first equation states that the limit as x approaches 1 from the left (indicated by a superscript minus sign after the 1) of ƒ(x) equals 1. The second equation states that the limit as x approaches 1 from the right (indicated by the superscript plus sign after the 1) of ƒ(x) equals 2.

A formal definition for the left-hand limit might look like this:

Definition 1.2: Left-Hand Limit
Let ƒ(x) be defined on the open interval (α,x₀) (where α < x). Then the statement

means that for each ε > 0, there exists a δ > 0 such that

x₀ - δ < x < x₀ implies that y₀ - ε < ƒ(x) < y₀.■

A similar definition can be constructed for right-handed limits, where the last line would read:

x₀ < x < x₀ + δ implies that y₀ < ƒ(x) < y₀ + ε

It is possible for a one-sided limit not to exist. Such is the case for the function ƒ(x) = sin(1/x), which was seen in Lesson 1.3.

The Existence of a Limit


Theorem 1.1: The Existence of a Limit


The limit lim_x→x0 ƒ(x) exists if and only if both one-sided limits exist at that point and both one-sided limits are equal to each other. Furthermore, the value of the limit, if it exists, is equal to the value of either one-sided limit.■

If a function ƒ(x) is defined at x₀ and its limit exists at x₀, it does not follow that lim_x→x0 ƒ(x) = ƒ(x₀). For example, consider the function

The plot of this function is shown below:

Figure 1.5

I put the tick marks on the frame and omitted the axes so you could see a little clearer what is going on. You can see that there is a jump discontinuity at x = 0, where the function "jumps" from x² to 1 at x = 0. For this function, ƒ(0) = 1; however, lim_x→x0 ƒ(x) = 0.

We are now in a position to formally define the concepts of continuity and discontinuity.

Definition 1.3: Continuity


1. A function ƒ(x) is continuous at the point x₀ if and only if the function is defined at x₀ [i.e., ƒ(x₀) is defined], limit of the function exists at that point, and

2. Similar to point 1, a function is continuous from the left (or the right) at x₀ if it is defined at x₀, the left-sided (or right-sided) limit exists at that point, and the lim_x→x0^- = ƒ(x₀) [or lim_x→x0⁺ = ƒ(x₀)].

3. A function is continuous on an open interval (a, b) if and only if it is continuous at each point in the interval.

4. A function is continuous on a closed interval [a, b] if and only if it is continuous on the open interval (a, b) and it is continuous from the right at a and continuous from the left at b.

4. A function which is continuous on the interval (-∞, ∞) is said to be everywhere continuous.

5. A function that is not continuous at a point or on an interval is said to be discontinuous at that point or on that interval. Furthermore, a function that is discontinuous on the interval (-∞, ∞) is said to be everywhere discontinuous.■

The fourth statement in Definition 1.3 may seem a little funny, but there are indeed function which are everywhere discontinuous. One such function is the Dirichlet function, which is defined as:

Not only is the Dirichlet function everywhere discontinuous, but in fact, the limit of the function does not even exist at any point along the entire number line.

Types of Discontinuities

Discontinuities come in two flavors, removable discontinuities, and non-removable discontinuities. A discontinuity of ƒ(x) at x₀ is removable if it is possible to define or redefine ƒ(x₀) such that the function becomes continuous at that point.

The discontinuity in Figure 1.5 is removable because ƒ(0) can be redefined as ƒ(0) = 0 to make the function continuous. The discontinuity in Figure 1.4, however, is non-removable because there is no way to redefine ƒ(1) such that the function becomes continuous. Another form of non-removable discontinuity occurs when the function exhibits unbounded behavior. For example, the functions ƒ(x) = 1/x and ƒ(x) = 1/x^2 (Shown below in Figures 1.6 and 1.7) both have non-removable discontinuities at x = 0:

Figure 1.6

Figure 1.7

Figure 1.8

Recall the function ƒ₁(x) = (x⁴ - 1)/(x - 1) from Lesson 1.1, in which we factored the numerator into (x³ + x² + x + 1)(x - 1). This function (shown to the right in Figure 1.8) had a discontinuity at x = 1, which we removed by cancelling the factor (x - 1) from the numerator and denominator to get ƒ₂(x) = x³ + x² + x + 1, which is the same as ƒ₂(x), except it is continuous at the point x = 1, rather than being undefined at that point. In general, when a common factor can be cancelled in the numerator and the denominator, then the discontinuity that resulted from that factor being in the denominator is removable and can be removed by cancelling the factor.

Properties of Continuity

Theorem 1.2 Properties of Continuity


If b is a real number and ƒ and g are continuous at x = c, then the following functions are also continuous at c:

1. bƒ
2. ƒ ± g
3. ƒg
4. ƒ/g, provided g(c) ≠ 0

If g is continuous at c and ƒ is continuous at g(c), then the composite function (ƒ ◦ g)(x) = ƒ(g(x)) is continuous at c.■

Some types of function that are continuous at every point in their domain are polynomials, radical function [ƒ(x) = x^1/n, for integer n], and the trigonometric functions sin x, cos x, tan x, cot x, sec x, and csc x.

Theorem 1.3 The Intermediate Value Theorem


If ƒ is continuous on the closed interval [a, b], then ƒ(x) takes on every value between ƒ(a) and ƒ(b) at least once in that interval.■

Lesson 1.3: Utilizing the ε-δ Definition and Limits that Do Not Exist

Example 1.1


Use the ε-δ definition to show

(Feel free to try this one yourself before looking at the answer to see if you can get it.)

Solution: What we are asking here is to show that for each ε > 0, there exists a δ > 0 such that 0 < |x - 2| < δ implies that |x² - 4| < ε. The first thing to notice is that |x² - 4| = |x - 2||x + 2|.

Next, notice that in the interval 1 < x < 3, |x + 2| < 5. Because of this, if ε ≥ 5, we can simply choose δ = 1, which yields |x - 2| < 1. This, in conjunction with the fact that |x + 2| < 5 (remember, that when δ = 1, we are working on the interval (1, 3) on the x-axis) implies that |x + 2||x - 2| < |x + 2| < 5 ≤ ε.

Thus, if ε ≥ 5, then choosing δ = 1, yields¹

Next, we have to find an appropriate δ for ε < 5. In this case, ε/5 < 1. When we choose δ = ε/5 (since ε/5 < 1, the equation |x + 2| < 5 still applies), we get |x - 2| < ε/5. This means that |x - 2||x + 2| < (ε/5)(5) = ε. Thus, we have

Note that when ε = 5, both of the above two arguments apply, since δ = ε/5 = 1. From the above arguments, we conclude that whenever δ equals the minimum of 1 and ε/5 (in other words, whichever one is lowest), then the statement

is true. Since we have succeeded in finding a δ > 0 for each ε > 0 and for which the above statement is true, then we have also succeeded in proving the statement

■

Note that in the above example, it was rather cumbersome and not at all obvious how to initially go about proving the limit. It is even more difficult to use the ε-δ definition to find an unknown limit. Because of that, the  ε-δ definition is almost never used to find limits. Instead, more sophisticated techniques have been developed to determine limits, which will shortly be presented on this blog. Instead, the  ε-δ definition is really useful for proving properties of limits, which we will also get to shortly and whether specific types of limits exist. For now, I would like to present some limits whose odd behaviors prevent the limits from actually existing.

Differing Behavior From the Left and from the Right


Consider the function y = |x|/x. The plot of this function is shown in Figure 1.1

Figure 1.1

As you can see from Figure 1.1, ƒ(x) is -1 if x is negative, +1 if x is positive, or undefined if x = 0. The interesting thing here is obviously the plot differs from the left and the right of x = 0. Because the function gets arbitrarily close to -1 as x approaches 0 from the left, and arbitrarily close to +1 as x approaches 0 from the right, the limit, lim_x→0 (|x|/x) does not exist (as we shall see though, there are one-sided limits which do exist for this point on the function). Formally, for any open interval (-δ, δ) on the x-axis, there will always be values of x inside that interval for which ƒ(x) = 1 and values of x for which ƒ(x) = -1.

Unbounded Behavior

The plot for y = 1/x² is shown in Figure 1.2 below:

Figure 1.2

As x approaches 0, for this function, ƒ(x) increases without bound. The smaller the interval (-δ, δ), the bigger ƒ(x) must be within that interval. Since ƒ(x does not approach a real number as x approaches 0 (∞ is not a number), we say the limit lim_x→0 1/x² does not exist. In this particular case, however, we may write

This is not a statement of the existence of the limit, but rather a statement that the function increases without bound as x approaches 0. A limit must be equal to a finite number in order to be considered as existing.

Oscillating Behavior


There are many interesting functions for which limits at specific points (or all points) do not exist for various reasons. One final important behavior that prevents limits from existing are functions that have an infinite number of oscillations between two fixed values as x approaches x₀. An example of such a function is ƒ(x) = sin 1/x. Consider the following points of the function:

ƒ(2/π) = 1
ƒ(2/3π) = -1
ƒ(2/5π) = 1
ƒ(2/7π) = -1
ƒ(2/9π) = 1
etc...

In fact, there are an infinite number of oscillations between 1 and -1 on the y-axis for any open interval (-δ, δ) about x = 0. Because of this, the function never settles down to approach any given value no matter how small of an interval you consider. See Figure 1.3 below for a plot of the function.

Figure 1.3²

Footnotes

¹ The double-struck arrow in the notation below this line means "implies," and the upside-down A can be read as "for all," so, in this instance, the statement above reads "0 < |x - 2| < 1 implies (that) |x² - 4| < ε for all ε ≥ 5." Some authors use a single-struck, or normal arrow such as "→" to mean "implies." A left-pointing arrow can be read as "is implied by" indicating that the condition to the right of the arrow implies the condition to the left, rather than the other way around, and an arrow pointing both ways is used as shorthand for "iff," which itself is shorthand for "if and only if," which means that the right condition both implies the left condition and is implied by the left condition (in other words, if one of the two conditions is true, then they are both true).

² The title of Figure 1.3 should read, "ƒ(x) = sin(1/x)" and not "ƒ(x) = sin(x)"

Lesson 1.2: Formal Definition of a Limit (The ε-δ Defintion)

As I have alluded to in the previous post,lim_x→x0 ƒ(x) = y₀ means that as x approaches x₀, ƒ(x) gets arbitrarily close to y₀. The reason this is not considered a rigorous definition is because the phrases, "as x approaches x₀," and "ƒ(x) gets arbitrarily close to y₀" have not been formally defined. We should therefore, officially present a more rigorous definition for the limit called the ε-δ definition:

Definition 1.1: Limit


Let ƒ(x) be a function defined on an open interval containing x₀, except possibly at x₀ The statement

means that for each ε (Greek letter epsilon) > 0, there exists δ (Greek letter delta) > 0 such that

0 < |x - x₀| < δ implies that |ƒ(x - y₀| < ε. ■

To see what this definition means, we must deconstruct each inequality. The first inequality has two parts. The first part, 0 < |x - x₀| simply means x ≠ x₀.

The second part of the first inequality is |x - x₀| < δ and can be rewritten as -δ < x - x₀ < δ. Adding δ to all three sides, we get

In other words, x lies in the interval (x₀ - δ, x₀ + δ). Similarly, the second inequality can be rearranged and written as

So,the second inequality means that ƒ(x) lies in the interval (y₀ - ε, y₀ + ε). With this, we an get a clearer interpretation of the ε-δ definition:

Interpretation of Definition 1.1


Let ƒ(x) be a function defined on an open interval containing x₀, except possibly at x₀ The statement

means that for each open interval about y_0, I_y = (y₀ - ε, y₀ + ε), there exists an interval about x_0,  I_x = (x₀ - δ, x₀ + δ) such that

x₀ ∈ I_x implies that ƒ(x) ∈ I_y. ■

The symbol ∈ means "is contained in," or "is an element of." The following image is a graphical representation of the ε-δ definition. Notice that y₀ ± ε does not necessarily correspond to ƒ(x₀ ± δ); although if y₀ ± ε ≠ ƒ(x₀ ± δ), then it is necessary that the interval (y₀ - ε, y₀ + ε) must contain the interval (ƒ(x₀ - δ), ƒ(x₀ + δ)). In other words, (ƒ(x₀ - δ), ƒ(x₀ + δ)) ⊆ (y₀ - ε, y₀ + ε).

Lesson 1.1: The Concept of Limits

Let x₀ be in the domain of the function ƒ(x) and let y = ƒ(x). The limit of ƒ(x) means the value that ƒ(x) approaches, or gets closer and closer to (arbitrarily close to), as x approaches x₀. If y₀ is the limit of ƒ(x) as x approaches x₀, this can be written as:

As a simple example, take the function ƒ(x) = x² and let x₀ = 2. In this case, lim_x→2 (x²) = 4. What this means that as x approaches 2, ƒ(x) gets arbitrarily close to the value 4. To see what is happening here, imagine the graph of this function (which is a parabola opened up and passing through the origin):

If you take your finger and trace the curve in that graph, as you finger gets closer and closer to 2 along the x axis, it gets closer and closer to 4 along the y axis.

In this particular case,ƒ(x₀) = lim_x→x0 ƒ(x) (i.e., lim_x→2 (x²) = 4 = 2²). This is not always the case.

To see an example where this is not true, consider the function ƒ₁(x) = (x⁴ - 1)/(x - 1). This function is not defined for x = 1 (at x = 1, the denominator is zero). You can see this in the graph below, where a hole is in the plot of the function at x = 1:

Because this function is undefined at x = 1, in order to find the limit as x approaches 1, it is useful to calculate the function for values of x close to 1 on both sides and see if the numbers are trending to a specific value:

x	0.75	0.9	0.99	0.999	1	1.001	1.01	1.1	1.25
ƒ1(x)	2.734	3.439	3.940	3.994	undefined	4.006	4.060	4.641	5.766

As you can guess from the table above, as x approaches 1 from either side, ƒ₁(x) gets arbitrarily close to 4. Thus,

A bit of algebraic manipulation reveals that the numerator of this function can be factored as into (x³ + x² + x + 1)(x - 1). If we cancel x - 1 in the numerator with x - 1 in the denominator we get the function ƒ₂(x) = x³ + x² + x + 1. This function is identical to ƒ₁(x) except at the point x = 1, as you can see in the graph below:

As you have no doubt noticed, ƒ₂(1) = 4, and as you may have guessed, it is not a coincidence that lim_x→1 ƒ₁(x) = ƒ₂(1). We shall see the reason for this shortly.

Lesson 0: Quick Review of Functions

The domain of a function f(x) is the set of all values of x for which f(x) is defined. Most common functions of real numbers (unless otherwise noted, we shall stick to real numbers for the time being) have a range extending from -∞ to +∞¹. Some functions, however, do not have this full range. For example, the function

Only has a domain of [0, ∞) (also written as 0 ≤ x < ∞).

The range of a function are the value which the function can output. Again, many functions have a range that spans the entire real number line. Some functions, however, only have a limited range. The function f(x) = sin x, for example, only has a range of [-1, 1].

In the equation y = f(x), f(x) is considered a function if and only if for each value of x in its domain, there exists one and only one value for y.

A function can be defined explicitly or implicitly. The equation y = f(x) defines y as a function of x explicitly. However, as an example of a simple implicitly defined function, we can use the equation y + x = 1. This equation implicitly defines y as a function of x (in this particular case, x could also be said to be implicitly defined as a function of y). If we rearrange the equation, we can get y = 1 - x, which is of the form y = f(x) (y here is being defined explicitly as a function of x) where f(x) = 1 - x.

Not all equations, however, define a function. The equation for the unit circle centered on the origin, for example, is

This equation does not define a y as a function of x (and for the same reason, it does not define x as a function of y). To see why, we should rearrange the equation to get y by itself. To do this, we subtract x^2 from both sides and then take plus or minus the square root:

The reason we must take plus or minus the square root is because the result of the original equation remains unchanged if we change the value we have for y to its negative. For example [1/Sqrt(2)]^2 + [1/Sqrt(2)]^2 = [-1/Sqrt(2)]^2 + [1/Sqrt(2)]^2 = 1. The result is the same if we use plus or minus 1/Sqrt(2). Because this equation cannot find a unique value for y for each value of x in the domain, it is not a function. To visually see why this is, consider the graph of the unit circle:

For each value along the x (horizontal) axis, there are two values along the y (vertical) axis. The two exceptions are at the points x = 1 and x = -1. Take for example, x = 0 (the origin). You can choose to go up from the origin, and eventually hit the graph at the y value y = 1, or you can choose to go down from the origin and eventually hit the graph at y = -1. Because there are two value of y corresponding to most values of x, this fails to be a graph of a function (only one value of x corresponding to more than one y is enough for an equation or graph to not define a function).

Now we can choose to only take the positive values of y in the equation, which would correspond only to the top half of the circle, and this would define a function.

A visual test to see if a graph defines a function or not is to take a vertical line and pass it over the entire domain of the graph. If there is any point along the x axis in which the vertical line hits more than one point on the graph, then the graph does not define a function. If no such point exists, then the graph does define a function. This is called the vertical-line test.

I am here of course assuming an understanding of the basics of graphing. If anyone needs help with slopes and intercepts and tests for symmetry etc. let me know and I will try to accommodate. I will help with logarithms and exponentials, when the time comes, but I hate trig. so if anyone needs help with that, if you have a specific question, I could probably answer it, but most likely I will not dedicate a whole blog entry to it.

Most functions have inverses (pretty much an inverse can be defined in some form or another, if not explicitly); however, not all functions have inverse functions. That is to say that just because f(x) is a function does not mean that f ^ -1 (x) is a function. The example of the unit circle above shows, for example, the the inverse of the square (plus or minus the square root) is not a function. In general, is multiple values of x give the same value of y (which is permissible in functions), then its inverse is not a function. To visually see if the inverse of the graph of a function (or equation) is itself a function, one can perform a horizontal-line test (which is the same as the vertical line test, only with a horizontal line running along the entirety of the range of the graph).

My plan is to begin actual calculus on my next post by starting with the basics of limits.

Footnotes

¹ This range is expressed as (-∞, +∞) where the parentheses indicate an open interval (square brackets indicated a closed interval--since infinity is not a number, it is impossible to have the interval closed on a side with either positive or negative infinity). It can also be expressed as -∞ < x < +∞ (closed intervals will use a less than or equal to sign). 

Intro

This will be the first (hopefully) in a series of math and physics blogs that I intend to create as a way to make physics and higher-level math available and accessible to the general public for free. For now, I will assume a working knowledge of algebra, trigonometry, and geometry. If the need arises and time permitting I will create blogs to outline the basics of those areas of mathematics.

While I encourage people to ask questions about things they do not understand in the comments section, please understand that I am doing this for free in my spare time. I will try to answer as many questions as possible as quickly as possible, but I also have a full time job and other things going on in my life. So please respect that if I don't respond to your question right away.

I will try to make sure that all the information I post in this blog is considered common knowledge in math and science related academia. Graphs that I post will be produced with Mathematica (unless otherwise noted) and equations will be rendered using either Mathematica or (usually) Microsoft Word, which has a great process for rendering equations. I'm not sure how exactly integrating equations and graphs into my posts is going to work, so I may need to try a few times before getting my posts to look the way I want them to. If anyone feels I have mis-used copyrighted materials in any way, please inform me and I will take the appropriate actions.